Introdução:
O número de ouro não é mais do que um valor numérico cujo valor aproximado é 1,618. Este número irracional é considerado por muitos o símbolo da harmonia. A escola grega de Pitágoras estudou e observou muitas relações e modelos numéricos que apareciam na natureza, beleza, estética, harmonia musical e outros, mas provavelmente a mais
importante é a razão áurea, razão divina ou proporção divina. Se quiséssemos dividir um
segmento AB em duas partes, teríamos uma infinidade de maneiras de o fazer. Existe
uma, no entanto, que parece ser mais agradável à vista, como se traduzisse uma
operação harmoniosa para os nossos sentidos. Relativamente a esta divisão, o
matemático alemão Zeizing formulou, em 1855, o seguinte princípio: “Para que um todo dividido em duas partes desiguais pareça belo do ponto
de vista da forma, deve apresentar a parte menor e a maior a mesma relação
que entre esta e o todo."
Origem:
A história deste enigmático número perde-se na antiguidade. No Egito as
pirâmides de Gizé foram construídas tendo em conta a razão áurea: a razão entre a altura
de uma face e a metade do lado da base da grande pirâmide é igual ao número de ouro.
ou Ahmes que mede 5,5 metros de comprimento por 0,32 metros de largura, datado
aproximadamente no ano 1650 a.C. onde encontramos um texto matemático na forma de
manual prático que contém 85 problemas copiados em escrita hierática pelo escriba
Ahmes de um trabalho mais antigo. Refere-se a uma «razão sagrada» que se crê ser o
número de ouro. Esta razão ou seção áurea também aparece em muitas estátuas da
antiguidade.
Definição algébrica
A razão áurea é definida algebricamente como:
A equação da direita mostra que  o que pode ser substituído na parte esquerda, resultando em:
o que pode ser substituído na parte esquerda, resultando em:
 o que pode ser substituído na parte esquerda, resultando em:
o que pode ser substituído na parte esquerda, resultando em:
Cancelando b em ambos os lados, temos:
Multiplicando ambos os lados por  resulta:
resulta:
 resulta:
resulta:
Finalmente, subtraindo 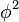 de ambos os membros da equação e multiplicando todas as parcelas por
de ambos os membros da equação e multiplicando todas as parcelas por  encontramos:
encontramos:
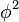 de ambos os membros da equação e multiplicando todas as parcelas por
de ambos os membros da equação e multiplicando todas as parcelas por  encontramos:
encontramos: que é uma equação quadrática da forma
que é uma equação quadrática da forma 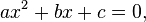 em que
em que 
Agora, basta resolver essa equação quadrática. Pela Fórmula de Bháskara:




A única solução positiva dessa equação quadrática é a seguinte:
 que é o número
que é o número 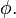
Música
O número de ouro está presente nas famosas sinfonias Sinfonia n.º 5 e a Sinfonia n.º 9, de Ludwig van Beethoven, e em outras diversas obras. Outro fato interessante registrado na Revista Batera, em um artigo sobre o baterista de jazz Max Roach, é que, em seus solos curtos, aparece tal número, se considerarmos as relações que aparecem entre tempos de bumbo e caixa. O compositor húngaro Béla Bartók utiliza esta relação de proporcionalidade constantemente em sua obra. Este fato pode ser visto na análise da música de Bartók feita por Ernö Lendvai (Béla Bartók: And Analysis of his Music).





Enzzo Matheus
ResponderExcluirKarine Kiss
Vanessa Raquel