Trabalho de Geo . 2 º ano Economia Zona da Mata

 Zona da Mata Paraibana

Sol e praia. Essa perfeita combinação parece ser a marca registrada do turismo na Paraíba. Para quem busca agitação, as praias urbanas de João Pessoa são a melhor opção. Além da estrutura de bares, restaurantes, e feiras de artesanato, o turismo encontra ainda passeio de barco até os recifes que acompanham quase toda a extensão da cidade. Um dos lugares mais visitados na capital é a Ponta do Seixas, o trecho de praia que mais se aproxima do continente africano em toda a América do Sul. Em Lucena, Baía da Traição, Mataraca e Barra de Mamanguape (litoral norte), aldeias indígenas cercadas por rios e mangues oferecem roteiros que misturam natureza e história num doa mais preservados trechos do litoral nordestino. No sul, o destaque é para Tambaba, primeira praia naturista do Nordeste.

Litoral

O Litoral da Paraíba se estende por cerca de 133 quilômetros. Sua extensão vai da desembocadura do rio Goiana - ao sul, onde se limita com o estado de Pernambuco - até o estuário do rio Guaju - ao norte, na divisa com o Rio Grande do Norte.
Lucena, Rio Tinto, marcação, Mamanguape, Baia da Traição e Mataraca são os municípios que englobam o Litoral Setentrional. O Litoral Sul abrange os territórios municipais de João Pessoa, Cabedelo, Bayeux, Santa Rita, Conde, Alharanda e Pitimbu. 

Gabriel Nunes De Oliveira Melo

Trabalho de Matemática

Trabalho de Geografia

Pecuária de Caprina Paraibana

A caprinocultura de leite é uma das principais atividades econômica da Paraíba, é fonte geradora de renda e de fixação do homem no campo. Este tipo de criação é mais intenso no Cariri Paraibano localizado na parte centro-sul da Paraíba.
A Paraíba é o maior produtor de leite de cabra no País, com uma produção média de meio milhão de litros por mês, produzida por criadores agregados em 22 associações rurais, na região do Cariri Paraibano.
Para suprir a grande demanda de leite e produtos associados do caprino, a Paraíba esta importando material genético da África e em 2010 o governo determinou que fosse elaborado outro programa de melhoramento genético(que já havia sido feito na Paraíba), sendo importado 1.000 embriões importados da África para dar um novo impulso no rebanho caprino Paraibano.
Um estudo foi feito pelo Sebrae sobre o “Mercado de carne derivados do caprino”,a Paraíba representa 6% dos rebanhos da Região Nordeste. O estado é o 5º no ranking regional, ficando atrás da Bahia, Pernambuco, Ceará e Piauí. A Região da Borborema apresenta o maior rebanho caprino, sendo o município de Monteiro o que concentra maior volume entre as cidades que desenvolve esse tipo de cultura.

Aluno: Matheus Moreira da Silva 

2º Ano

Professor: Lins

Trabalho de Matemática

 Grupo: Débora Félix
Luara Wenere
Vitória Gilvanda
Série: 2° ano

Numeros de ouro

               A segmentação ou proporção áurea é um dos mais eficientes recursos existentes de proporcionalidade estética. Foi amplamente utilizada através de toda a História da Arte. Os antigos egípcios já conheciam esta relação e a usaram na construção das pirâmides, também os gregos em seus templos, os grandes artistas em suas pinturas e esculturas e os mestres da música em suas composições.

Introdução:

           O número de ouro não é mais do que um valor numérico cujo valor aproximado é 1,618. Este número irracional é considerado por muitos o símbolo da harmonia. A escola grega de Pitágoras estudou e observou muitas relações e modelos numéricos que apareciam na natureza, beleza, estética, harmonia musical e outros, mas provavelmente a mais 

importante é a razão áurea, razão divina ou proporção divina. Se quiséssemos dividir um 

segmento AB em duas partes, teríamos uma infinidade de maneiras de o fazer. Existe 

uma, no entanto, que parece ser mais agradável à vista, como se traduzisse uma 

operação harmoniosa para os nossos sentidos. Relativamente a esta divisão, o 

matemático alemão Zeizing formulou, em 1855, o seguinte princípio: 

“Para que um todo dividido em duas partes desiguais pareça belo do ponto 

de vista da forma, deve apresentar a parte menor e a maior a mesma relação 

que entre esta e o todo."

Origem: 

              A história deste enigmático número perde-se na antiguidade. No Egito as 

pirâmides de Gizé foram construídas tendo em conta a razão áurea: a razão entre a altura 

de uma face e a metade do lado da base da grande pirâmide é igual ao número de ouro.

              Outro exemplo da proporção áurea na antiguidade é o Papiro de Rhind (Egípcio) 
ou Ahmes que mede 5,5 metros de comprimento por 0,32 metros de largura, datado 
aproximadamente no ano 1650 a.C. onde encontramos um texto matemático na forma de 
manual prático que contém 85 problemas copiados em escrita hierática pelo escriba 
Ahmes de um trabalho mais antigo. Refere-se a uma «razão sagrada» que se crê ser o 
número de ouro. Esta razão ou seção áurea também aparece em muitas estátuas da 
antiguidade.

Definição algébrica

A razão áurea é definida algebricamente como:

A equação da direita mostra que  o que pode ser substituído na parte esquerda, resultando em:

Cancelando b em ambos os lados, temos:

Multiplicando ambos os lados por  resulta:

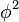Finalmente, subtraindo  de ambos os membros da equação e multiplicando todas as parcelas por encontramos:

 que é uma equação quadrática da forma 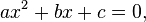 em que 

Agora, basta resolver essa equação quadrática. Pela Fórmula de Bháskara:

A única solução positiva dessa equação quadrática é a seguinte:

 que é o número 

Música

               O número de ouro está presente nas famosas sinfonias Sinfonia n.º 5 e a Sinfonia n.º 9, de Ludwig van Beethoven, e em outras diversas obras. Outro fato interessante registrado na Revista Batera, em um artigo sobre o baterista de jazz Max Roach, é que, em seus solos curtos, aparece tal número, se considerarmos as relações que aparecem entre tempos de bumbo e caixa. O compositor húngaro Béla Bartók utiliza esta relação de proporcionalidade constantemente em sua obra. Este fato pode ser visto na análise da música de Bartók feita por Ernö Lendvai (Béla Bartók: And Analysis of his Music).