Trabalho de Química

Trabalho de Química
Grupo: Luara Wenere
Débora Cristina
Vitória Gilvanda

"Paródia Química"

Trabalho de Química do 2° ano
Grupo: Jeyse Christynne
Letícia Maria
Bettina Maia
Joany Leandro
José Felipe
José Lucas
Lucas E. Souto
Matheus Moreira

ESPANHOL

Espanhol - Trabalho sobre Salvador

Trabalho realizado pelos alunos do 3º ano, sobre os pontos turísticos de Salvador.

TRABALHO DE ESPANHOL - 3º ANO QI-Sul

Trabalho de Espanhol dos alunos do 3º ano sobre os pontos turísticos de João Pessoa.

Geografia - Lins - Agreste

Aluno: Lucas Emmanuel Anizio
Qi Litoral Sul
2° ano

Agreste

         É a região intermediária entre a Mata e o Sertão. Caracteriza-se por uma economia diversificada, com o cultivo de lavouras como milho , feijão, mandioca, entre outras, e pecuária leiteira e de corte. Principal bacia leiteira do Estado, o Agreste tem índices pluviométricos maiores que os do Sertão, com média anual entre 800 e 1000 milímetros, mas também é uma região sujeita a secas periódicas.

Está dividida em seis microrregiões, que veremos a seguir: Vale do Ipanema, Vale do Ipojuca, Alto Capibaribe, Médio Capibaribe, Garanhuns e Brejo Pernambucano. Tem, em geral, solos rasos, já erodidos e depauperados e presta-se para o cultivo de cereais.

Situada no Agreste pernambucano, ocupa uma área de 5.274 km2, é formada por 06 municípios, apresenta clima semi-árido, com temperaturas elevadas, chuvas escassas e mal distribuídas e rios temporários.

A economia da microrregião tem como base a pecuária extensiva (nos vastos pediplanos) e menos extensiva em algumas áreas, além de lavouras de subsistência. Os municípios mais populosos são Águas Belas e Buíque.

Composta por 16 municípios, é a microrregião do Agreste pernambucano que possui estrutura urbana mais consolidada, com razoável dinamismo no setor industrial e comercial, sobressaindo-se a cidade de Caruaru, que é a maior cidade do interior do Estado e um centro comercial de importância interregional. As maiores indústrias, com destaque para os setores de alimentos e confecções, estão nos municípios de Caruaru, Pesqueira e Belo Jardim.

A microrregião tem atividades agrícolas diversificadas, destacando-se as culturas de tomate, beterraba, cenoura, repolho, alface, pimentão e outras, sobretudo nas áreas de brejo, onde se sobressaem os municípios de Brejo da Madre de Deus e Gravatá.

É uma microrregião do Agreste pernambucano, formada por 09 municípios e tem uma área de 1.608 km2, equivalente a 1,63% do território estadual. A economia da maioria dos municípios depende de atividades rurais, com exceção de Santa Cruz do Capibaribe (foto ao lado) e Surubim que, juntos, detém quase 70% da taxa de urbanização da microrregião.

A cidade de Santa Cruz do Capibaribe desenvolveu, a partir dos anos 1970, uma atividade que nada tem a ver com a base econômica regional: é a confecção de vestuário, pruduzida através de inúmeras microempresas que geram renda e emprego para a maioria da população da cidade.

Cálculo da Quantidade de ar em uma lata

Trabalho de Geo . 2 º ano Economia Zona da Mata

 Zona da Mata Paraibana

Sol e praia. Essa perfeita combinação parece ser a marca registrada do turismo na Paraíba. Para quem busca agitação, as praias urbanas de João Pessoa são a melhor opção. Além da estrutura de bares, restaurantes, e feiras de artesanato, o turismo encontra ainda passeio de barco até os recifes que acompanham quase toda a extensão da cidade. Um dos lugares mais visitados na capital é a Ponta do Seixas, o trecho de praia que mais se aproxima do continente africano em toda a América do Sul. Em Lucena, Baía da Traição, Mataraca e Barra de Mamanguape (litoral norte), aldeias indígenas cercadas por rios e mangues oferecem roteiros que misturam natureza e história num doa mais preservados trechos do litoral nordestino. No sul, o destaque é para Tambaba, primeira praia naturista do Nordeste.

Litoral

O Litoral da Paraíba se estende por cerca de 133 quilômetros. Sua extensão vai da desembocadura do rio Goiana - ao sul, onde se limita com o estado de Pernambuco - até o estuário do rio Guaju - ao norte, na divisa com o Rio Grande do Norte.
Lucena, Rio Tinto, marcação, Mamanguape, Baia da Traição e Mataraca são os municípios que englobam o Litoral Setentrional. O Litoral Sul abrange os territórios municipais de João Pessoa, Cabedelo, Bayeux, Santa Rita, Conde, Alharanda e Pitimbu. 

Gabriel Nunes De Oliveira Melo

Trabalho de Matemática

Trabalho de Geografia

Pecuária de Caprina Paraibana

A caprinocultura de leite é uma das principais atividades econômica da Paraíba, é fonte geradora de renda e de fixação do homem no campo. Este tipo de criação é mais intenso no Cariri Paraibano localizado na parte centro-sul da Paraíba.
A Paraíba é o maior produtor de leite de cabra no País, com uma produção média de meio milhão de litros por mês, produzida por criadores agregados em 22 associações rurais, na região do Cariri Paraibano.
Para suprir a grande demanda de leite e produtos associados do caprino, a Paraíba esta importando material genético da África e em 2010 o governo determinou que fosse elaborado outro programa de melhoramento genético(que já havia sido feito na Paraíba), sendo importado 1.000 embriões importados da África para dar um novo impulso no rebanho caprino Paraibano.
Um estudo foi feito pelo Sebrae sobre o “Mercado de carne derivados do caprino”,a Paraíba representa 6% dos rebanhos da Região Nordeste. O estado é o 5º no ranking regional, ficando atrás da Bahia, Pernambuco, Ceará e Piauí. A Região da Borborema apresenta o maior rebanho caprino, sendo o município de Monteiro o que concentra maior volume entre as cidades que desenvolve esse tipo de cultura.

Aluno: Matheus Moreira da Silva 

2º Ano

Professor: Lins

Trabalho de Matemática

 Grupo: Débora Félix
Luara Wenere
Vitória Gilvanda
Série: 2° ano

Numeros de ouro

               A segmentação ou proporção áurea é um dos mais eficientes recursos existentes de proporcionalidade estética. Foi amplamente utilizada através de toda a História da Arte. Os antigos egípcios já conheciam esta relação e a usaram na construção das pirâmides, também os gregos em seus templos, os grandes artistas em suas pinturas e esculturas e os mestres da música em suas composições.

Introdução:

           O número de ouro não é mais do que um valor numérico cujo valor aproximado é 1,618. Este número irracional é considerado por muitos o símbolo da harmonia. A escola grega de Pitágoras estudou e observou muitas relações e modelos numéricos que apareciam na natureza, beleza, estética, harmonia musical e outros, mas provavelmente a mais 

importante é a razão áurea, razão divina ou proporção divina. Se quiséssemos dividir um 

segmento AB em duas partes, teríamos uma infinidade de maneiras de o fazer. Existe 

uma, no entanto, que parece ser mais agradável à vista, como se traduzisse uma 

operação harmoniosa para os nossos sentidos. Relativamente a esta divisão, o 

matemático alemão Zeizing formulou, em 1855, o seguinte princípio: 

“Para que um todo dividido em duas partes desiguais pareça belo do ponto 

de vista da forma, deve apresentar a parte menor e a maior a mesma relação 

que entre esta e o todo."

Origem: 

              A história deste enigmático número perde-se na antiguidade. No Egito as 

pirâmides de Gizé foram construídas tendo em conta a razão áurea: a razão entre a altura 

de uma face e a metade do lado da base da grande pirâmide é igual ao número de ouro.

              Outro exemplo da proporção áurea na antiguidade é o Papiro de Rhind (Egípcio) 
ou Ahmes que mede 5,5 metros de comprimento por 0,32 metros de largura, datado 
aproximadamente no ano 1650 a.C. onde encontramos um texto matemático na forma de 
manual prático que contém 85 problemas copiados em escrita hierática pelo escriba 
Ahmes de um trabalho mais antigo. Refere-se a uma «razão sagrada» que se crê ser o 
número de ouro. Esta razão ou seção áurea também aparece em muitas estátuas da 
antiguidade.

Definição algébrica

A razão áurea é definida algebricamente como:

A equação da direita mostra que  o que pode ser substituído na parte esquerda, resultando em:

Cancelando b em ambos os lados, temos:

Multiplicando ambos os lados por  resulta:

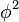Finalmente, subtraindo  de ambos os membros da equação e multiplicando todas as parcelas por encontramos:

 que é uma equação quadrática da forma 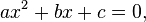 em que 

Agora, basta resolver essa equação quadrática. Pela Fórmula de Bháskara:

A única solução positiva dessa equação quadrática é a seguinte:

 que é o número 

Música

               O número de ouro está presente nas famosas sinfonias Sinfonia n.º 5 e a Sinfonia n.º 9, de Ludwig van Beethoven, e em outras diversas obras. Outro fato interessante registrado na Revista Batera, em um artigo sobre o baterista de jazz Max Roach, é que, em seus solos curtos, aparece tal número, se considerarmos as relações que aparecem entre tempos de bumbo e caixa. O compositor húngaro Béla Bartók utiliza esta relação de proporcionalidade constantemente em sua obra. Este fato pode ser visto na análise da música de Bartók feita por Ernö Lendvai (Béla Bartók: And Analysis of his Music).

Enem 2012: Redação

Observem estas dicas, no mais, é só lembrar das nossas aulas! Sucesso.

11 dicas dos corretores da redação do Enem 2012 - 1. Proposta e textos motivadores

Não esqueça de ler com atenção a proposta de redação e os textos motivadores (os textos de apoio que aparecem antes da proposta). Desta maneira, você compreenderá bem o que está sendo solicitado e não fugirá do tema, evitando, portanto, que sua redação seja "zerada".

11 dicas dos corretores da redação do Enem 2012 - 2. Criatividade

Evite ficar preso às ideias desenvolvidas pnos textos motivadores. Elas foram apresentadas apenas para despertar a sua criatividade e uma reflexão sobre o tema. Ou seja, crie argumentos novos, mostre que você sabe mais do que apenas copiar uma ideia já apresentada.

11 dicas dos corretores da redação do Enem 2012 - 3. Não copie

Não copie trechos dos textos motivadores. Lembre-se de que eles foram apresentados apenas para despertar seus conhecimentos sobre o tema.

11 dicas dos corretores da redação do Enem 2012 - 4. Reflexão

Reflita sobre o tema proposto para decidir como abordá-lo, qual será seu ponto de vista e quais os argumentos que vai utilizar para defendê-lo.

11 dicas dos corretores da redação do Enem 2012 - 5. Reunir ideias

Reúna todas as ideias que ocorrerem sobre o tema, procurando organizá-las em uma estrutura coerente para usá-las no desenvolvimento do seu texto.

11 dicas dos corretores da redação do Enem 2012 - 6. Desenvolver

Desenvolva o tema de forma consistente, de modo que o leitor possa acompanhar seu raciocínio facilmente, o que significa que a progressão textual é fluente e articulada com o projeto do texto.

11 dicas dos corretores da redação do Enem 2012 - 7. Tópico frasal

Lembre-se de que cada parágrafo deve desenvolver um tópico frasal. Ou seja, uma frase-chave, que deve ser o carro-chefe da ideia apresentada no parágrafo. É recomendado que você comece o parágrafo com o tópico frasal.

11 dicas dos corretores da redação do Enem 2012 - 8. Coerência

Examine com atenção a introdução e a conclusão para ver se há coerência entre o início ou fim. Ou seja, garanta que você defende os mesmos pontos apresentados no começo até o fim da redação.

11 dicas dos corretores da redação do Enem 2012 - 9. Conhecimento

Os corretores também querem conteúdo de você. Por isso, utilize informações de várias áreas do conhecimento, demonstrando que você está atualizado em relação ao que acontece no mundo.

11 dicas dos corretores da redação do Enem 2012 - 10. Clichês

Evite falar o que tudo mundo já sabe. Não aposte em reflexões previsíveis, que demonstram pouca originalidade no desenvolvimento do tema proposto.

11 dicas dos corretores da redação do Enem 2012 - 11. Fuga do tema

Mantenha-se dentro dos limites do tema proposto, tomando cuidado para não se afastar do foco. Esse é um dos principais problemas identificados nas redações. Nesse caso, duas situações podem ocorrer: fuga total ou parcial ao tema.

Fonte: Universia Brasil

Experimentos Químicos Caseiros

Trabalho de Química
Alunas: Vitória Gilvanda
Luara Wenere
Débora Felix

Video das meninas.

Conservação da quantidade de movimento

Grupo: Weslley Rhaonny, Jalyson Rahony, Samuel Melo, Bruno de Lucas e Wagner da Silva

   No século XVIII um pirata chamado Jack Sparrow estava no Pérola negra com sua tripulação em uma batalha de navios contra a tripulação do Capitão Barbossa, quando Jack disparou com seu canhão de 2 toneladas um projétil de 8 kg, que lança o projétil  a 900km/h [ 250 m/s] atingindo o outro navio.
   Com essas informações calcule a velocidade do recuo da peça, desprezando a ação de forças externas.                                                 
                                                                                 PROCEDIMENTOS:

   1.   Represente a peça de artilharia e a bala antes e depois do disparo;
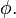
   2.   Utilize o princípio da conservação da quantidade de movimento. antes =depois (observar a orientação).                                         

                                                   

VP- velocidade da peça

VB - velocidade da bala

antes =depois

0   = - v_P ·2000 + 8 ·250

2000 v_p = 2000

v_p = 1 m/s